After creating a text classifier on Part 1 of this series of analysis on Table Tennis equipment, there is another aspect of choosing equipment that is tricky: making sense of all the specs of rubbers. Luckily, Revspin.net has user-generated data we can use for this. Characteristics like Speed, Spin, Control, Gears, Tackyness are rated from 1 to 10 for a big number of rubbers. The issue with this is that is very hard to make sense of all those numbers, Revspin does not offer a comparison tool currently, and even if it did, typical 1-to-1 comparison toolsfall short when you want to find similar products.
With the goeal of making product discovery and recomendation easier, I analysed data from the Top 100 rated rubbers on Revspin to build a recomendation tool using unsupervised learning techniques. Let’s jump to the code!
data = pd.read_csv('top100 rubbers by overall score.csv')
data.head()
| Rubber | Speed | Spin | Control | Tacky | Weight | Sponge Hardness | Gears | Throw Angle | Consistency | Durable | Overall | Ratings | Estimated Price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Donic Bluestorm Z1 Turbo | 9.4 | 9.7 | 8.5 | 1.2 | 6.0 | 8.8 | 9.4 | 4.4 | 10.0 | 7.8 | 9.6 | 6 | $ 52.00 |
| 1 | Tibhar Aurus TC-1 | 8.9 | 9.6 | 9.4 | 2.0 | 4.4 | 3.2 | 10.0 | 5.2 | 10.0 | 9.0 | 9.5 | 5 | $ 28.00 |
| 2 | Xiom Omega VII Tour | 9.6 | 9.3 | 8.4 | 1.9 | 7.5 | 8.3 | 9.1 | 6.0 | 10.0 | 7.8 | 9.5 | 15 | $ 74.00 |
| 3 | DHS Gold Arc 8 | 9.4 | 9.4 | 9.2 | 2.1 | 5.8 | 6.8 | 8.8 | 5.7 | 9.6 | 8.8 | 9.5 | 100 | $ 46.00 |
| 4 | Adidas Tenzone Ultra | 9.3 | 9.5 | 9.0 | 2.3 | 5.3 | 7.2 | 8.6 | 6.5 | 9.7 | 8.6 | 9.5 | 18 | $ 50.00 |
data.dtypes
Rubber object
Speed float64
Spin float64
Control float64
Tacky float64
Weight float64
Sponge Hardness float64
Gears float64
Throw Angle float64
Consistency float64
Durable float64
Overall float64
Ratings int64
Estimated Price object
dtype: object
Initial Exploration and clustering Link to heading
We can use pair plots to explore posible clusters in the data, next I run pair plots only for Speed, Spin and Control to keep it manageable. They are also the most important aspects on a rubber so it’s all good.
import seaborn as sns
sns.pairplot(data[['Speed','Spin','Control']])
<seaborn.axisgrid.PairGrid at 0x7fbe945e9f10>
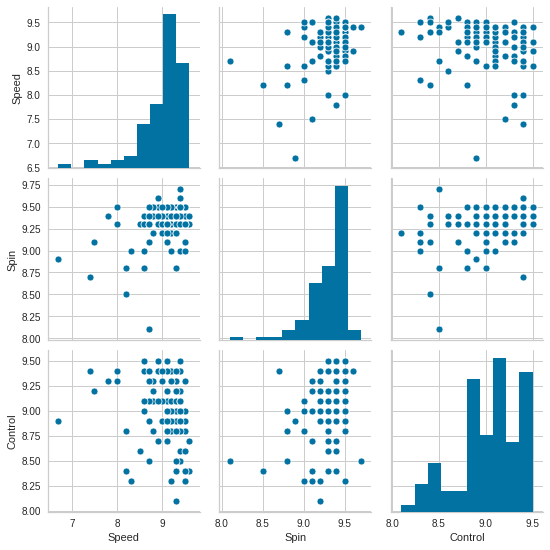
Below is an initial clustering using Speed vs Spin
kmeans = cluster.KMeans(8)
kmeans.fit(data[['Speed', 'Spin']])
labels = kmeans.labels_
fig = px.scatter(data, x="Speed", y="Spin",
color=labels, hover_data=['Rubber','Estimated Price'], title='Speed vs Spin')
fig.show()
Exploring clusters Link to heading
data['cluster'] = kmeans.labels_
data.sort_values(by='cluster',ascending=False).head(10)
| Rubber | Speed | Spin | Control | Tacky | Weight | Sponge Hardness | Gears | Throw Angle | Consistency | Durable | Overall | Ratings | Estimated Price | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 73 | Haifu White Shark II (2) (Tuned) | 8.7 | 8.1 | 8.5 | 2.2 | 3.7 | 2.8 | 6.8 | 3.5 | 7.5 | 5.5 | 9.4 | 13 | $ 26.00 | 7 |
| 64 | Nittaku Hurricane Pro III Turbo Blue | 8.5 | 9.3 | 8.6 | 8.4 | 8.2 | 9.5 | 9.4 | 5.3 | 8.9 | 7.7 | 9.4 | 11 | $ 45.00 | 6 |
| 82 | Gewo Proton Neo 375 | 8.6 | 9.3 | 9.4 | 0.4 | 2.4 | 3.0 | 7.5 | 6.6 | 10.0 | 8.7 | 9.4 | 11 | $ 42.00 | 6 |
| 35 | TSP Ventus Spin | 8.8 | 9.4 | 9.2 | 1.5 | 2.8 | 3.1 | 8.5 | 5.9 | 9.6 | 8.3 | 9.4 | 48 | $ 48.00 | 6 |
| 37 | Tibhar Grip-S | 8.8 | 9.5 | 8.8 | 7.1 | 6.5 | 6.6 | 8.6 | 6.2 | 8.8 | 7.5 | 9.4 | 25 | $ 45.00 | 6 |
| 38 | DHS Gold Arc 3 | 8.8 | 9.2 | 9.3 | 5.3 | 5.7 | 6.6 | 9.5 | 5.3 | 9.1 | 8.5 | 9.4 | 14 | $ 39.00 | 6 |
| 40 | TSP Ventus Soft | 8.7 | 9.4 | 9.4 | 1.5 | 2.1 | 1.4 | 8.4 | 6.5 | 9.5 | 8.1 | 9.4 | 26 | $ 42.00 | 6 |
| 25 | Adidas P7 | 8.8 | 9.5 | 9.1 | 2.1 | 4.4 | 6.5 | 9.1 | 6.1 | 9.4 | 8.4 | 9.4 | 79 | $ 50.00 | 6 |
| 61 | Tibhar Genius Sound | 8.7 | 9.5 | 8.9 | 2.7 | 3.5 | 2.6 | 7.3 | 6.1 | 9.4 | 7.2 | 9.4 | 59 | $ 46.00 | 6 |
| 32 | Gewo NanoFLEX FT40 | 8.6 | 9.4 | 9.5 | 1.2 | 3.7 | 2.9 | 8.0 | 7.5 | 10.0 | 8.7 | 9.4 | 20 | $ 60.00 | 6 |
Dimensionality Reduction with PCA Link to heading
Clustering by Speed/Spin is good, but we’re missing a lot of information like Tackiness, Weight, Gears and others. We’ll now use Principal Component Analysis (PCA) to perform dimensionality reduction with the intention of exploring the data in 2D.
%time
data2 = pd.read_csv('top100 rubbers by overall score.csv')
data2["Rubber"]=data2['Rubber'].str.strip()
data2.index = data2['Rubber']
data_pca = data2.drop(columns=['Rubber','Ratings','Estimated Price']).copy()
CPU times: user 6 µs, sys: 0 ns, total: 6 µs
Wall time: 11.4 µs
%time
x = data_pca.values
x = StandardScaler().fit_transform(x)
CPU times: user 4 µs, sys: 0 ns, total: 4 µs
Wall time: 6.91 µs
%time
pca = PCA(n_components=2, random_state=2020)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents
, columns = ['Component_1', 'Component_2'], index=data_pca.index)
CPU times: user 6 µs, sys: 1 µs, total: 7 µs
Wall time: 11.2 µs
principalDf.sample(5)
| Component_1 | Component_2 | |
|---|---|---|
| Rubber | ||
| Andro Rasant Turbo | -1.203339 | 0.666231 |
| Gewo Proton Neo 325 | 4.443144 | -2.770060 |
| Adidas P7 | -0.406847 | -0.847028 |
| Andro Rasanter R47 | -0.885781 | 0.296568 |
| Tibhar Rapid X-Press | 1.257376 | 5.263687 |
principalDf = principalDf.join(data2['Estimated Price'])
principalDf.sample(5)
| Component_1 | Component_2 | Estimated Price | |
|---|---|---|---|
| Rubber | |||
| Tibhar 5Q Update | -0.080693 | -0.542226 | $ 58.00 |
| Gewo NanoFLEX FT45 | 0.366319 | -1.396074 | $ 45.00 |
| Nittaku Renanos Hold | 0.077362 | 0.392463 | $ 40.00 |
| Victas VS > 401 | -0.806909 | -0.272544 | $ 41.00 |
| Butterfly Tenergy 05 | -1.044239 | 1.074280 | $ 72.00 |
Now we have columns Factor 1 and Factor 2 that we can use for plotting purposes. I added price for an extra point of comparison.
Clustering with Principal Components Link to heading
kmeans = cluster.KMeans(7)
kmeans.fit(principalDf[['Component_1', 'Component_1']])
labels = kmeans.labels_
principalDf['Rubber'] = principalDf.index
fig = px.scatter(principalDf, x="Component_1", y="Component_2",
color=labels, hover_data=['Rubber','Estimated Price'])
fig.show()
#Exploring clusters
principalDf['Group'] = kmeans.labels_
principalDf.sort_values(by=['Group','Estimated Price'],ascending=False).head(10)
| Component_1 | Component_2 | Estimated Price | Rubber | Group | |
|---|---|---|---|---|---|
| Rubber | |||||
| Gewo NanoFLEX FT40 | 1.542088 | -2.691248 | $ 60.00 | Gewo NanoFLEX FT40 | 6 |
| Donic Acuda Blue P2 | 0.952946 | 0.385298 | $ 54.00 | Donic Acuda Blue P2 | 6 |
| Andro Rasant Powersponge | 1.776572 | -0.835600 | $ 53.00 | Andro Rasant Powersponge | 6 |
| Xiom Omega 3 Asian | 1.100396 | 2.167658 | $ 50.00 | Xiom Omega 3 Asian | 6 |
| TSP Ventus Spin | 1.455195 | -1.529631 | $ 48.00 | TSP Ventus Spin | 6 |
| Tibhar Grip-S Europe Soft | 0.877569 | 2.127313 | $ 45.00 | Tibhar Grip-S Europe Soft | 6 |
| Gewo Nexxus EL Pro 43 | 1.214484 | -1.156517 | $ 45.00 | Gewo Nexxus EL Pro 43 | 6 |
| Tibhar Rapid X-Press | 1.257376 | 5.263687 | $ 44.00 | Tibhar Rapid X-Press | 6 |
| Andro Hexer Powergrip SFX | 1.623274 | -0.209761 | $ 41.00 | Andro Hexer Powergrip SFX | 6 |
| Andro Rasanter R42 | 0.936585 | -0.898905 | $ 38.00 | Andro Rasanter R42 | 6 |
# Instantiate the KElbowVisualizer with the number of clusters and the metric
visualizer = KElbowVisualizer(kmeans, k=(2,15) ,timings=False)
# Fit the data and visualize
visualizer.fit(x)
visualizer.poof()
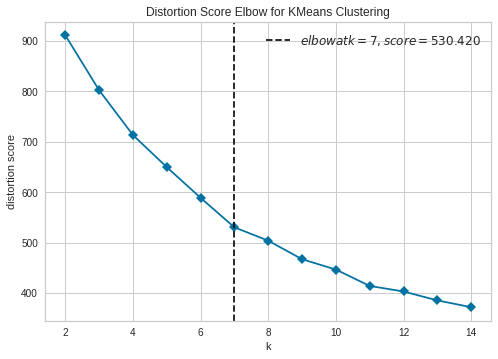
<matplotlib.axes._subplots.AxesSubplot at 0x7fbe8df7a650>
principalDf = principalDf.reset_index(drop=True)
principalDf['Rubber'] = principalDf['Rubber'].str.strip() #Fixing whitespaces
K-Nearest Neighbors Link to heading
Now we build our unsupervised KNN model to build our recommender
%time
knn_model = NearestNeighbors()
knn_model.fit(principalDf[['Component_1', 'Component_2']].values)
CPU times: user 6 µs, sys: 0 ns, total: 6 µs
Wall time: 12.2 µs
NearestNeighbors(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
radius=1.0)
Exploring Similar Rubbers with KNN Link to heading
At this point we have a model that maps our 2D space we created with PCA. KNN allow us to access the closest points given an initial one and since we condensed all the rubber characteristics into 2 features, our model effectively gives us the most similar rubbers given an initial one. Now we can use this to recommend similar rubbers! Let’s try with the famouse Butterfly Tenergy 05
rubber_name = 'Butterfly Tenergy 05' #Rubber to explore
rubber_point = principalDf[principalDf['Rubber']==rubber_name][['Component_1','Component_2']].values
%time
#Getting Neighbors
kneighbors = knn_model.kneighbors(rubber_point,n_neighbors=11)
kneighbors #Note how it gives us the distance and an index list sorted by it
CPU times: user 9 µs, sys: 1e+03 ns, total: 10 µs
Wall time: 17.6 µs
(array([[0. , 0.4379683 , 0.52560896, 0.60282679, 0.67766423,
0.68223504, 0.68839685, 0.72638111, 0.75281269, 0.79369034,
0.79785331]]),
array([[97, 44, 88, 80, 42, 24, 38, 62, 46, 75, 48]]))
#Creating a mapping to sort the data based on the distance to the coordinates of interest.
sorter_temp = kneighbors[1][0]
sorterIndex = dict(zip(sorter_temp,range(len(sorter_temp))))
knn_df_sorted = principalDf[principalDf.index.isin(sorter_temp)].copy() #Matching the kneighbors to get the rest of the data
knn_df_sorted['Similarity Rank'] = knn_df_sorted.index.map(sorterIndex)
similar_rubbers = knn_df_sorted.join(data, rsuffix='_r').sort_values(by=['Similarity Rank'])
similar_rubbers.drop(columns=['Component_1','Component_2','Rubber_r', 'Estimated Price_r'], inplace=True)
similar_rubbers
| Estimated Price | Rubber | Group | Similarity Rank | Speed | Spin | Control | Tacky | Weight | Sponge Hardness | Gears | Throw Angle | Consistency | Durable | Overall | Ratings | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 97 | $ 72.00 | Butterfly Tenergy 05 | 0 | 0 | 9.3 | 9.4 | 8.4 | 2.4 | 6.6 | 6.2 | 8.8 | 7.5 | 9.3 | 7.9 | 9.3 | 325 | 4 |
| 44 | $ 43.00 | Andro Rasant Turbo | 5 | 1 | 9.5 | 9.1 | 8.4 | 1.4 | 6.1 | 7.0 | 8.9 | 5.1 | 9.4 | 9.0 | 9.4 | 38 | 2 |
| 88 | $ 78.00 | Butterfly Tenergy 25 | 0 | 2 | 9.1 | 9.1 | 8.7 | 2.4 | 6.9 | 6.7 | 8.5 | 4.2 | 10.0 | 8.2 | 9.3 | 70 | 2 |
| 80 | $ 33.00 | Tibhar Evolution MX-P | 5 | 3 | 9.5 | 9.3 | 8.6 | 2.3 | 6.5 | 7.0 | 8.6 | 5.7 | 9.1 | 7.2 | 9.4 | 111 | 4 |
| 42 | $ 41.00 | JOOLA Maxxx 500 | 5 | 4 | 9.4 | 9.3 | 9.2 | 2.5 | 6.4 | 8.4 | 8.3 | 7.3 | 9.2 | 7.5 | 9.4 | 16 | 4 |
| 24 | $ 50.00 | Tibhar Evolution MX-S | 5 | 5 | 9.2 | 9.5 | 9.1 | 2.4 | 6.7 | 7.7 | 8.9 | 5.4 | 9.1 | 7.5 | 9.4 | 84 | 0 |
| 38 | $ 39.00 | DHS Gold Arc 3 | 0 | 6 | 8.8 | 9.2 | 9.3 | 5.3 | 5.7 | 6.6 | 9.5 | 5.3 | 9.1 | 8.5 | 9.4 | 14 | 6 |
| 62 | $ 60.00 | Xiom Omega IV Pro | 0 | 7 | 9.3 | 9.3 | 8.8 | 2.4 | 5.5 | 6.8 | 8.8 | 4.8 | 9.3 | 8.5 | 9.4 | 80 | 4 |
| 46 | $ 44.00 | Tibhar Aurus Prime | 5 | 8 | 9.5 | 9.5 | 8.9 | 2.6 | 5.5 | 7.0 | 9.0 | 6.6 | 8.6 | 8.2 | 9.4 | 27 | 4 |
| 75 | $ 47.00 | Andro Rasanter R47 | 0 | 9 | 9.4 | 9.3 | 9.0 | 1.8 | 5.7 | 6.4 | 9.0 | 6.1 | 9.4 | 7.5 | 9.4 | 71 | 4 |
| 48 | $ 44.00 | Donic Acuda Blue P1 | 0 | 10 | 9.3 | 9.2 | 8.9 | 2.8 | 4.9 | 6.2 | 8.7 | 5.9 | 9.4 | 7.4 | 9.4 | 24 | 2 |
Here we can see some results after testing the model with Tenergy 05. Overall the recomendations make sense, after a quick google search many of the rubbers shows up as good Tenergy alternatives like Tibhar MX-P or Xiom Omega IV Pro.
Conclusion Link to heading
It’s always very nice to see the effectivenses of traditional ML tools like PCA and KNN. Working on this is also a good reminder of the importance of knowing your data, it was easy for me think about what next step made sense given the data and that intuition was useful to evaluate the final results as well.
The next step on this project is to build an actual tool people can use to explore the data. I’m looking forward to it. Stay tunned.